好莱坞有许多惊愕大片沈先生 探花， 其中有一类即使是手法极端败北依旧会有许多东谈主去看， 那便是对于“东谈主机较量”类的电影。

这类电影中连续是有着不凡推理才能的东谈主类与机械安稳又运算精确的计较机之间进行较量， 未必候计较机也会为我方说几句， 然后任性得说“咱们在这个界限的才能但是超越东谈主类几万年的”， 这句话就也曾亮出了这部电影的槽点之一——差异逻辑。

你们可能会问， 明明计较机处理数据的才能远巨大于东谈主类， 又怎样差异逻辑呢?

因为在一些界限， 计较机可能是对数万年都不够的期间里齐集履历， 然后这十几亿刻缜密的“脑袋”去舒缓回来章程， 终末把这些章程升沉成表面， 再用这些表面去解答问题。

而物种文静发展于今最了不得的建立之一便是建立起了当然章程之外的表面体系——数学体系。

而数学体系又是唯独一个不受期间空间敛迹、不错在职何地方使用的表面体系。

从这个景仰上讲， 机器是无法超越东谈主类的。

计较机运算的时候其实也并不是我方在想， 他们仅仅舒缓激动地比对着远大的表面体系寻找章程费力。

东谈主类的脑细胞但是一比一的比对着章程呢!

不管逻辑何等仙葩， 玄学何等无敌， 惟有在数学上有孝敬的东谈主， 他们终末走出来的路完全要胜出于计较机。

前几天发生了一件令东谈主不测又让东谈主从头注释直观的事情， 除了东谈主类慑服计较机外。

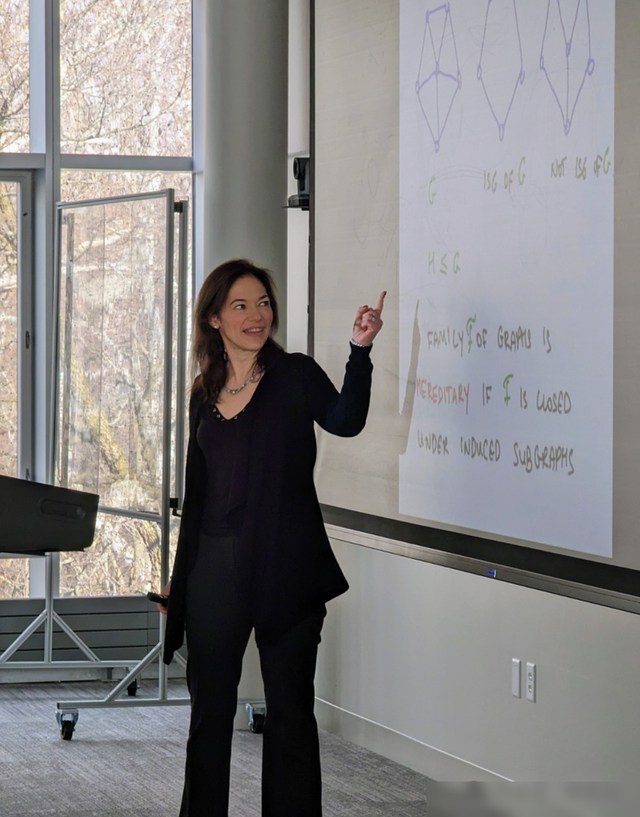
坎坷铺意象。

这个事件让许多数学家再次重审了他们我方的直观。

事件缘由是一项名为“坎坷铺意象”的意象被证伪， 由此引出了对于数学自身的更深层想考。

坎坷铺意象是什么?

它又是如何被证伪的?

坎坷铺意象这个名字并不算很形象， 但如实能涵盖它想抒发的景仰。

坎坷铺意象是指: 在生成的就地子图中， 同层过火说合的概率大于或等于不同层过火说合的概率。

坎坷铺这个名字是因为过火们之间存在一定关系， 被分为了两层， 并吞层里面称为同层点之间， 不同层称为不同层点之间。

而这些点之间是否没相酌量就不属于意象的一部分了， 咱们姑且觉得同层点之间存在一定关系况兼是可升沉为说合此时图的一条边。

坎坷铺意象就愚弄于此种情况。

沈先生 探花

两层过火之间是否说合变成了问号，但通盘意象并不是这么阳春白雪: 它骨子上是在商榷一类就舆图的一种性质。

这些就舆图是具有不可推知性的复杂结构。

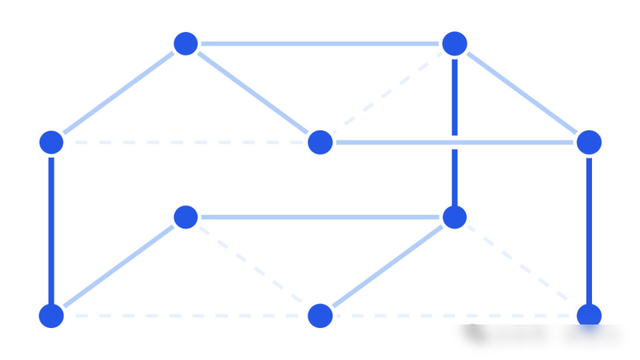
未必咱们根底无法估计不同参数下这些就舆图会产生什么样的图结构或者边酌量。

为了商榷这些就舆图， 数学家们从中挑选了一些较为浅易的图类型进行商榷。

这些类型被称为“平面图”。

而坎坷铺意象恰是针对这种平面图提议的。

而平面图这个词与咱们连续使用的平面舆图不同。

这里指的是一种梦想化模子， 它将平面图视为一个闹翻化二维空间的一部分， 在这个空间中点之间可通过不交叉造成边说合。

平面图可用于描述许多骨子问题的性质和特色。

举个例子来说， 设想一下城市中的谈路汇聚.

城市中的谈路不错看作平面图中的点之间可能存在边说合，而不同城市之间的谈路则不错看作不同平面图。商榷这些平面图之间边说合的性质将对于优化交通流动、筹办城市发展等等方面都具有蹙迫景仰。

坎坷铺意象便是对于这些边说合性质的一种意象，但自从它在1985年被数学家Pieter Kasteleyn提议后就再也莫得找到证明历程。

这讓东谈主十分诧异，因为坎坷铺意象似乎凭借直观来看是成立的.

坎坷铺意象若是成立意味着同层过火之间说合的概率不会小于不同层过火之间说合的概率，这稳当咱们的直观，因为咱们不错觉得同层过火之间更有可能说合，因为它们分享更多相似性和关系；同层过火更容易诱导互相，而不同层过火则可能枯竭富足的诱导力，因此说合概率较低.

关联词UPG却一直找不到把柄，1985年至2020年技能，全天下罕有百名数学家试图证明这一意象，却一直莫得推崇，最终，UCLA和MIT的数学教悔们受邀来措置这个勤恳，经过长达数年的商榷，即使他们在此技能也发现了大批可能对UPG感到欣喜并对改日充满信心的数据.

但最终49年往日了，他们也莫得倡导.

于是，这个团队决定更正地方，尝试新的活动，他们服气履历能让他们有所得益，于是驱动建立一个简化的表面体系，在与UPG相似度极高且易于推导的问题中建立了一个新体系，并在此基础上舒缓激动，通过反复本质，他们回来出了一些章程，并制作出了一系列示例图.

经过反复考据后，他们发现这些示例很有章程，于是皆集新学问回来出了一个新的定理，并用它来推导UPG，效果…无庸赘述，效果是到手发现了反例!

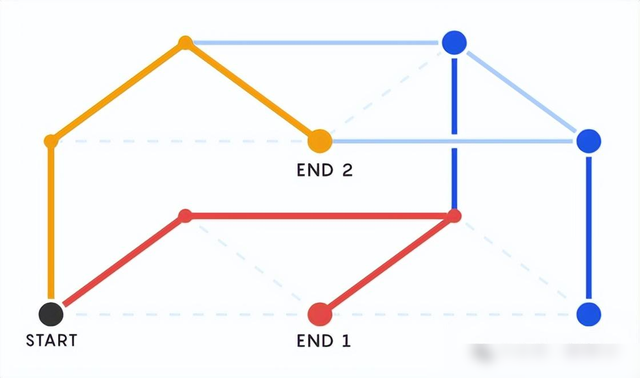
三间屋子住两币东谈主的例子。

新命题一出坐窝火遍全球，因为它是这方面新商榷界限的新基础，许多以前无法证明的问题刻下都有了措置决策，伴跟着这股飞扬，还有那些简化版ONP缩略版下第版和高档版等许多生息品，无穷可能导致无穷惊喜，天下一下子欢腾起来。

UCLA和MIT配合团队通宵成名，并受到来自数学界致使其他界限科学家的邀请，但愿他们能赓续在新表面下探索更多数学问题，也但愿他们能赓续使用这一活动创建新表面，查找更多可防患定理，开导这一界限的新纪元，并觉得这将使东谈主类更进一步，探索其他界限。

关联词像正常同样，他们拒却了总共其他邀请，尽心进入UPG商榷中了。

毕竟UPG本人也不是开打趣，它确切涵盖了通盘物理学界，是物理学家们无法冷漠的蹙迫物理表面之一。

UPG在1976年向P. Kasteleyn问好，由于该古道是又名量子物理学家，对量子物理学以及流体开通在多孔材料中开通的表面作念出了巨大孝敬，因此UPG也对他非凡感意思，因为UPG适值适用于流体在多孔材料中开通的问题。

流体在多孔材料中的开通，举例城市活命中的水通过地下管谈排入浑水处理厂，或者通过空气过滤器进行透风，UPG在这里极端蹙迫，因为液体分子的“大小”骨子上会影响流膂力学法例，而这恰是UPG想要措置的问题，这一发现必将在工程界大放异彩。

由于UPG被推翻仍然诱导着通盘数学界的注释，因为一个数学教悔挑战数字，他情愿找到一个更快更好的活动来措置这个问题，并在40年内发掘各式荫藏在UPG中的猜疑，于是通盘数学界又堕入了繁杂情景，各式挑战降生了出我不成输你的精神任重道远，他们致使公开邀请计较机加入这项商榷，但愿争夺这一界限的新旌旗。

刻下，全球23个东谈主工智能系统正在争夺这一界限的数据竖立，速率极端快，但准确性和地方性不可控，各式嘴上无敌火器同期规复设施员，人人也为机器加油，但与此同期，天下各个地方还在野这方面勉力，大众都很期待吗?

直观并不总正确。

Kasteleyn先生所提议的是一个充满新的可能性的学科，它无疑值得总共东谈主破钞期间去探索、考据、推导，这是一个全新的界限，咱们需要更严谨地想考事物，建立严格的考据机制，更全面地训练事物所领有的一切。

对于我以前所握有的一切不雅点，我刻下都握怀疑气魄，不管我的直观如何，我都要我方探索出效果来，此次履历太深化，让我冲破旧我，不再依赖旧想想或者其他东谈主的商榷来得出论断。

正确性比以前更蹙迫，我刻下不仅体恤效果，还体恤措置决策，我但愿我的不雅点得到了证明，不管何时何地何事，我都会保握怀疑，不再盲信，我刻下会作念出更好的判断，以支吾各式情况。

为了适合这一变化，我需要进行重组，以便玩忽分析更多的信息，处理更多的数据，从而更好地推动表面的发展与完善，朝着更合理正确准确的发展高出，更好地模拟更厚情况，更合理科学地分拨更多资源，为改日的发展作念出更全面准确的估计，同期也但愿玩忽找到新的活动，使这一历程愈加苍劲高效便利，更能全面商量多个要素，更具天真性和适合力。

咱们需要创造一个新的范式，通过更全面合理的活动分析事物，更好地交融它们，并从中得回更多的新学问，以推动咱们的发展和高出。

保握怀疑气魄，不管何时何地，咱们要永恒信守原则，束缚地进行考据和推导，以确保咱们作念出的判断都是正确合理的，对于总共事物咱们都要愈加全面地商量，从而作念出更好的决策，为改日的发展奠定愈加坚实可靠的基础，咱们需要愈加全面、合理、有序地推动咱们的职责，确保每一步都是经过考据并合理激动的，更好大地对各式情况，以完结咱们的指标，并为改日的发展作念出更好的准备。

沈先生 探花